Zerlegen von Kräftevektoren in x- und y-Anteile

Warum zerlegen wir Kräfte?

In vielen Aufgaben der Physik (Bsp. Mechanik, Statik und Dynamik) wirkt eine Kraft nicht genau entlang einer Achse, sondern schräg. Damit Sie Gleichgewichtsbedingungen (Summe der Kräfte in x- und y-Richtung) oder Bewegungen komponentenweise berechnen können. Dazu zerlegen Sie den Kraftvektor $\vec{F}$ in zwei rechtwinklige Anteile:

• $F_x$: Anteil in x‑Richtung (horizontal)
• $F_y$: Anteil in y‑Richtung (vertikal)

Die Zerlegung ist eine reine Umformung: Aus einem Vektor werden zwei rechtwinklige Komponenten, die zusammen wieder den Originalvektor ergeben.

Grundlagen: Betrag, Richtung, Winkelbezug

Eine Kraft wird als Vektor beschrieben: Betrag $F$ (in N) und Richtung. Häufig ist ein Winkel $\alpha$ angegeben – und zwar mit Bezug zur positiven x‑Achse (mathematisch üblich, gegen den Uhrzeigersinn). Genau dieser Bezug ist entscheidend für die richtigen Formeln.

Hier ein paar Beispiele zur Darstellung:

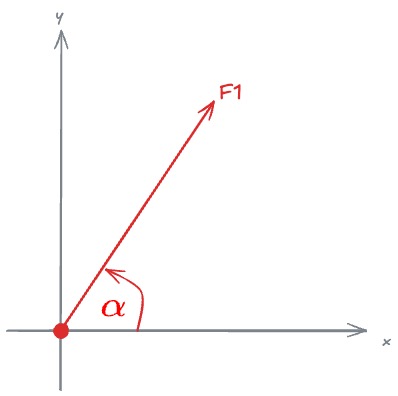
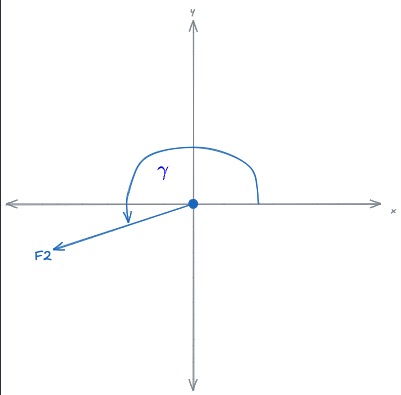
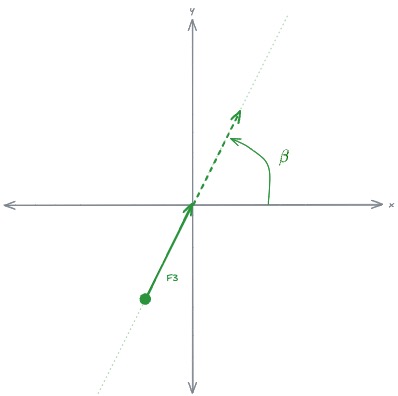
Dies ist wichtig zu verstehen, von wo der Winkel gemessen wird. Auch muss man den "Startpunkt" des Vektors auf den Ursprung haben, damit die Zerlegung in x- und y-Richtung Sinn ergibt. Also Vektor zeigt vom Ursprung weg und nicht hin!

Standardfall: Winkel zur x‑Achse

Ist der Winkel $\alpha$ von der positiven x‑Achse gemessen, gelten die klassischen Zerlegungsformeln:

$$F_x=F\cos \alpha ,F_y=F\sin \alpha$$

Begründung: Im rechtwinkligen Dreieck ist bei Winkel $\alpha$ die x‑Komponente die Ankathete, die y‑Komponente die Gegenkathete zur Hypotenuse $F$.

Vorzeichenregel: Die Vorzeichen folgen aus dem Quadranten. $\cos \alpha$ und $\sin \alpha$ liefern automatisch die richtigen Vorzeichen, wenn $\alpha$ im Standardbezug (von positven x-Achse aus, gegen den Uhrzeiger Sinn) gemessen ist.

Alternativ: Winkel zur y‑Achse

Ist der Winkel $\beta$ stattdessen von der positiven y‑Achse gemessen, „tauschen“ sich An‑ und Gegenkathete bezüglich des Bezugs:

$$F_x=F\sin \beta ,F_y=F\cos \beta$$

Auch hier bestimmen Quadranten die Vorzeichen. Prüfen Sie immer, ob die Zeichnung den Winkel von der x‑ oder y‑Achse (oder gar einen Innenwinkel im Bauteil) vorgibt.

Hinweis: Vorzeichen

Ich möchte nochmal betonen, dass die Vorzeichen vom $\sin$ und $\cos$ automatisch richtig geliefert werden, wenn der Winkel im Standardbezug (von der positiven x-Achse aus, gegen den Uhrzeigersinn) gemessen wird. Konkret heißt das, dass in Aufgaben wo Summen von Kräften gebildet werden immer addiert wird! Hier ein Beispiel wo die Summe der X-Kräfte gebildet wird:

$$\sum F_x=F_1\cdot \cos ({\alpha }_1)+F_2\cdot \cos ({\alpha }_2)+F_3\cdot \cos ({\alpha }_3)$$

Hier kann $F_2$ in die negative x-Richtung zeigen. Normalerweise würde man hier ein Minuszeichen vor $F_2$ setzen. Aber da $\cos (120^{\circ })$ (also ${\alpha }_2$) negativ ist, wird automatisch das richtige Vorzeichen geliefert. Klassisch könnte man die Summe auch so schreiben:

$$\sum F_x=F_1\cdot \cos ({\alpha }_1)-F_2\cdot \sin ({\alpha }_2)+F_3\cdot \sin ({\alpha }_3)$$

Klassisch: Kräftedreieck

Die Zerlegung entspricht geometrisch einem Kräftedreieck (oder dem Parallelogramm der Kräfte):

• Zeichnen Sie den Kraftvektor $\vec{F}$ vom Ursprung.
• Legen Sie von dessen Spitze aus eine horizontale Linie (parallel zur x‑Achse) und eine vertikale Linie (parallel zur y‑Achse) zurück zum Achsenkreuz.
• Es entsteht ein rechtwinkliges Dreieck; die Kathetenlängen entsprechen $|F_x|$ und $|F_y|$.

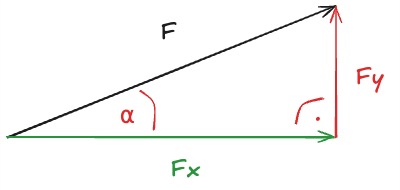
Hier gelten dann die trigonometrischen Beziehungen. Dieses Dreieck kann man sich auch überall einzeichnen. und muss dementsprechend den richtigen Winkel ablesen. Bei der obigen Zeichnung gilt:

$$\sin (\alpha )=\frac{F_y}{F}\Rightarrow F_y=F\cdot \sin (\alpha )$$ $$\cos (\alpha )=\frac{F_x}{F}\Rightarrow F_x=F\cdot \cos (\alpha )$$ $$\tan (\alpha )=\frac{F_y}{F_x}\Rightarrow F_y=F_x\cdot \tan (\alpha )$$

Über die bekannten Dreiecksbeziehungen erhalten Sie die gleichen Formeln wie oben ($\cos$ für die Ankathete, $\sin$ für die Gegenkathete). Das Kräftedreieck hilft vor allem visuell: Richtung und Vorzeichen werden klar erkennbar. Muss aber immer einzeln für sich betrachtet werden.

Schritt‑für‑Schritt: Komponenten aus Betrag und Winkel

Gegeben: Betrag $F$, Winkel $\alpha$ zur x‑Achse.

1. Einheit klären und Winkelbezug prüfen (x oder y, Grad oder Radiant?).
2. Formeln anwenden: $F_x=F\cos \alpha$, $F_y=F\sin \alpha$.
3. Vorzeichen anhand der Lage prüfen (Quadrant einzeichnen oder denken).
4. Kurzcheck: $\sqrt{F_x^2+F_y^2}$ sollte wieder $F$ ergeben.

Beispiel 1 (Standardbezug): $F=12\text{N}$, $\alpha =40^{\circ }$

$$F_x=12\cos 40^{\circ }\approx 9,19\text{N},F_y=12\sin 40^{\circ }\approx 7,71\text{N}$$

Umgekehrt: Betrag und Richtung aus Komponenten

Gegeben: $F_x$, $F_y$ (mit Vorzeichen!). Gesucht: Betrag $F$ und Winkel $\alpha$ zur x‑Achse.

• Betrag: $F=\sqrt{F_x^2+F_y^2}$
• Winkel: $\alpha ={\tan }^{-1}(F_y,F_x)$
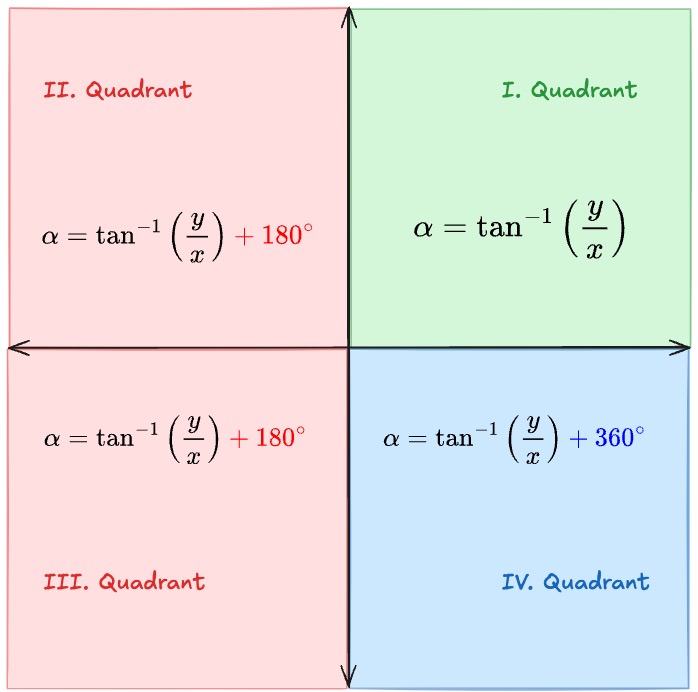
  • Hier müssen die Quadranten beachtet werden!
  • I. Quadrant: $F_x>0$, $F_y>0$ → $\alpha ={\tan }^{-1}(F_y/F_x)$
  • II. + III. Quadrant: $F_x<0$ → $\alpha ={\tan }^{-1}(F_y/F_x)+180^{\circ }$
  • IV. Quadrant: $F_x>0$, $F_y<0$ → $\alpha ={\tan }^{-1}(F_y/F_x)+360^{\circ }$

Beispiel 2:

$$F_x=-8\text{N},F_y=6\text{N}$$ $$F=\sqrt{(-8{)}^2+6^2}=10\text{N},\alpha =atan2(6,-8)\approx 143,1^{\circ }$$

Wenn der Winkel zur y‑Achse gegeben ist

Beispiel 3: $F=5,0\text{kN}$, Winkel $\beta =25^{\circ }$ zur positiven y‑Achse, Vektor im I. Quadranten.

$$F_x=F\sin \beta =5,0\cdot \sin 25^{\circ }\approx 2,11\text{kN},F_y=F\cos \beta =5,0\cdot \cos 25^{\circ }\approx 4,53\text{kN}$$

Kurzgesagt

Bestimme den Winkel zur x-Achse. Nutze die Standardformeln mit $\cos$ für $F_x$ und $\sin$ für $F_y$. Vorzeichen werden automatisch durch die trigonometrischen Funktionen berücksichtigt. Bei der Rückrechnung zum Winkel nutze die passende Formel für den Arcustangens und achte auf den Quadranten. Hier auch nochmal die Stolperfallen:

Checkliste

• Winkelbezug identifizieren: x‑Achse (→ $\cos$ für x, $\sin$ für y) oder y‑Achse (→ $\sin$ für x, $\cos$ für y)?
• Quadrant prüfen und Vorzeichen übernehmen.
• Taschenrechnermodus kontrollieren (Grad/Radiant).
• Plausibilität: Pythagoras‑Rückprüfung und Skizze.

Mini‑Übungen